Data Visualization and Exploration

Axes, Boxplots, and Histograms

Introduction

Recap

Differences between .Rmd and .qmd

code block options and syntax
header options
referencing and linking
output formats

Similarities? Pretty much everything else of relevance.

Recap (2)

A variety of graph options and auxillary functions.
Discussion about axes.
“Small multiples” vs. multiline graph.

Break upload files to D2L

Ensure your main files are named according to the convention lastname-firstname-basename.<ext>
Use your computer or downloaded utility to create a .zip file of the main directory
Upload the .zip file (format lastname-firstname-basename.zip) to the relevant D2L Assignments folder.

Catalog of links and notes

To follow.

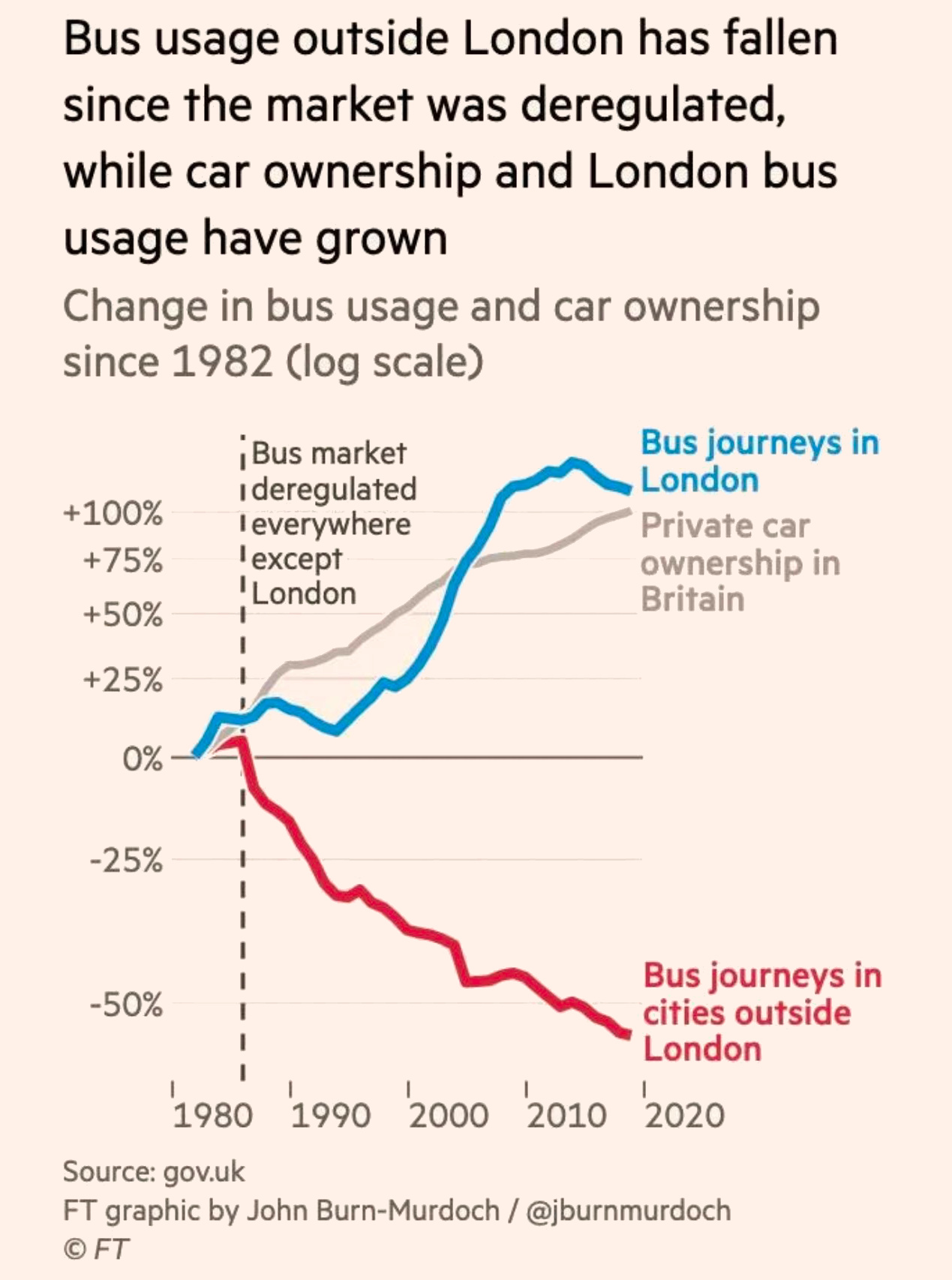
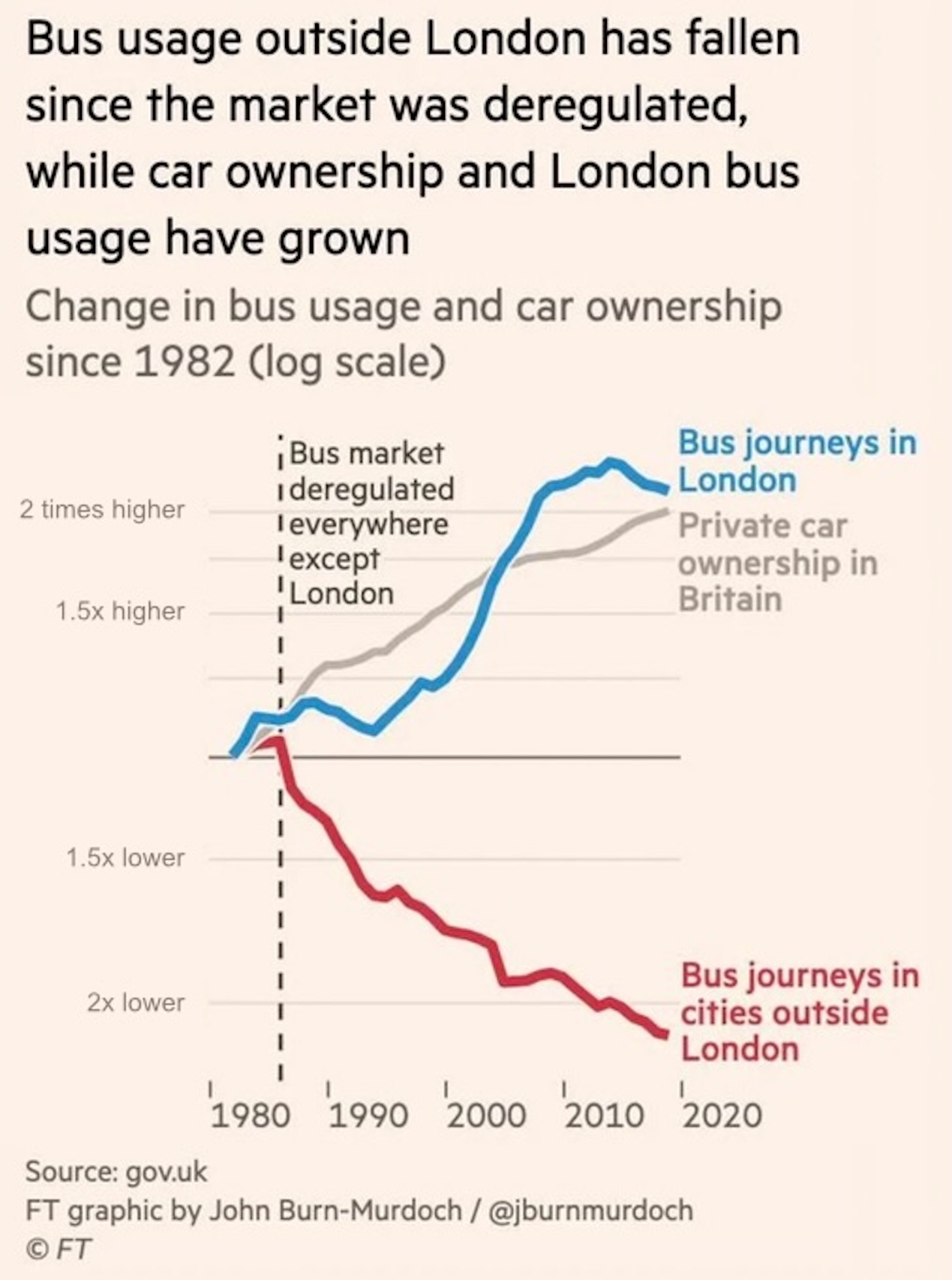
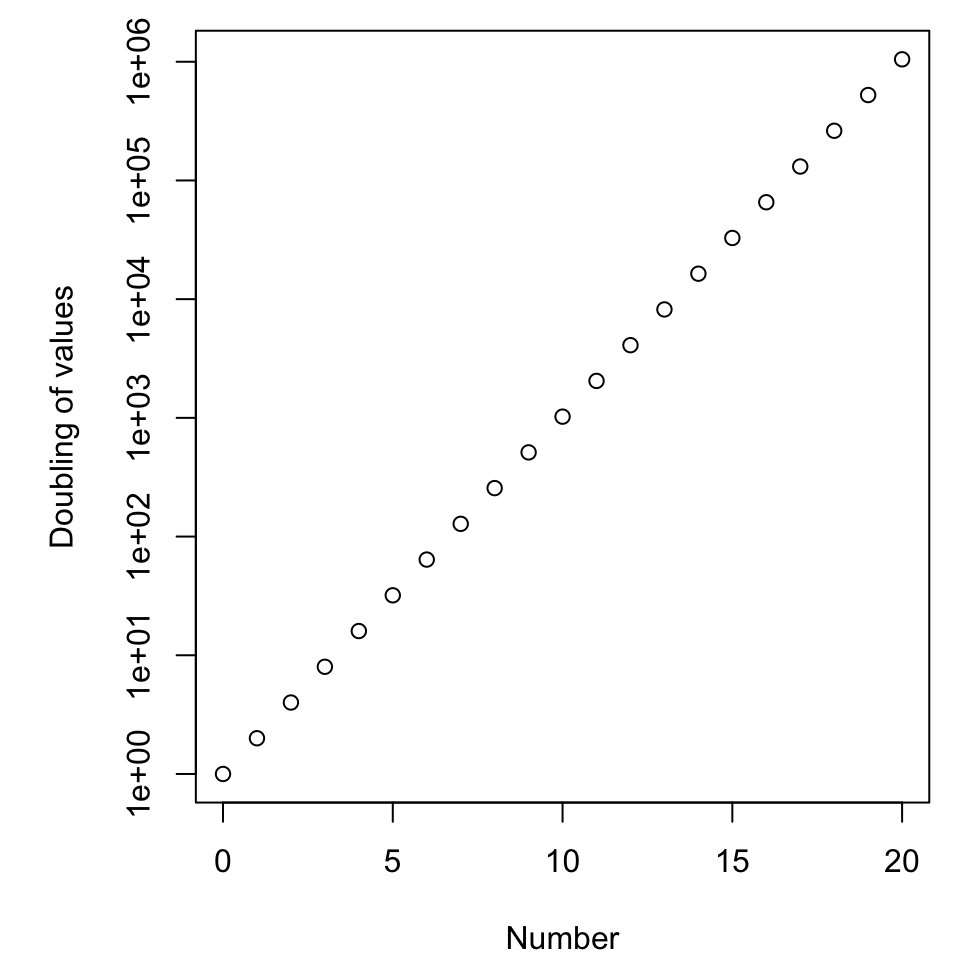
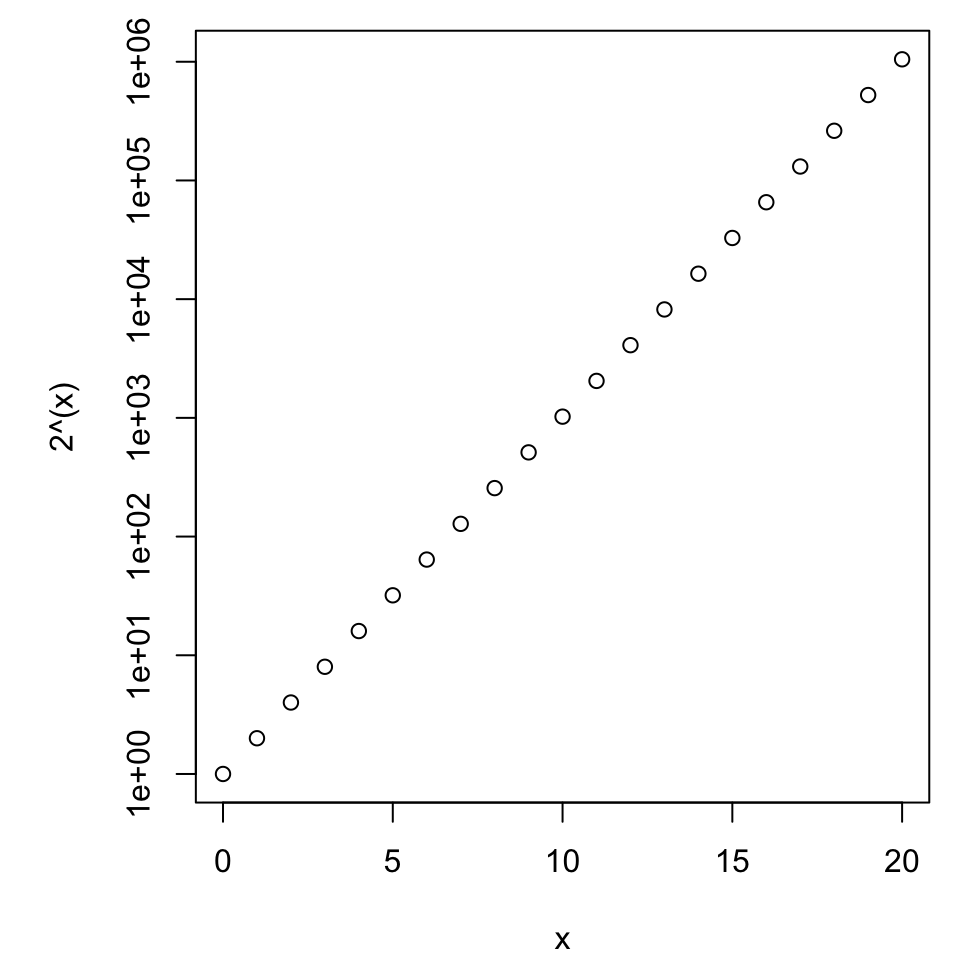
Axis scales

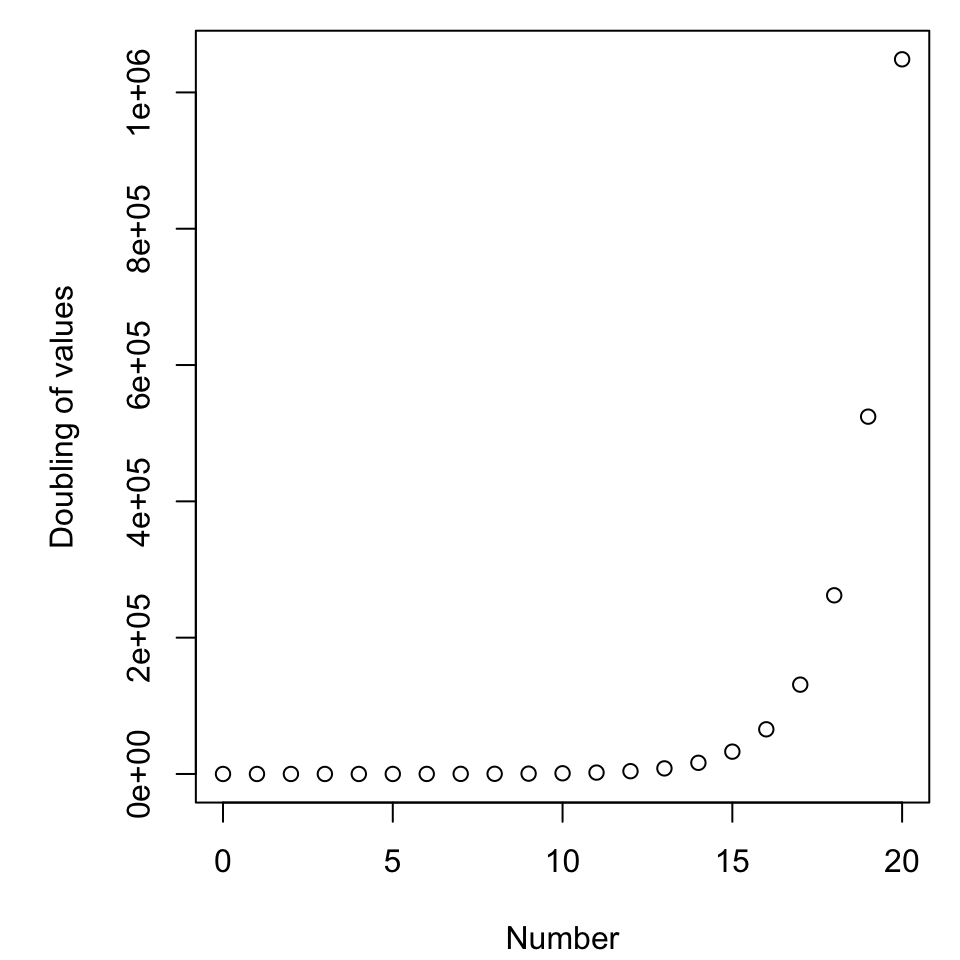
Exponential growth

Read in the data exponential.csv, give it a brief inspection, and make a plot that shows all three trials plotted against time. This could be done

column-by-column, or
all at once with matplot().

dat <- read.delim("./data/exponential.csv", header = T, sep = ',')
head(dat)
#>   time trial1 trial2  trial3
#> 1    0     10     10 10.0000
#> 2    1     10     20  5.0000
#> 3    2     10     40  2.5000
#> 4    3     10     80  1.2500
#> 5    4     10    160  0.6250
#> 6    5     10    320  0.3125

A closer look

Now plot just the first two rows. You can do this within the plot by putting a 1:2 in the first rows position of the data frame.

As measured by space, how much attention is given to halving versus doubling?
Is this fair?

Enter log scales

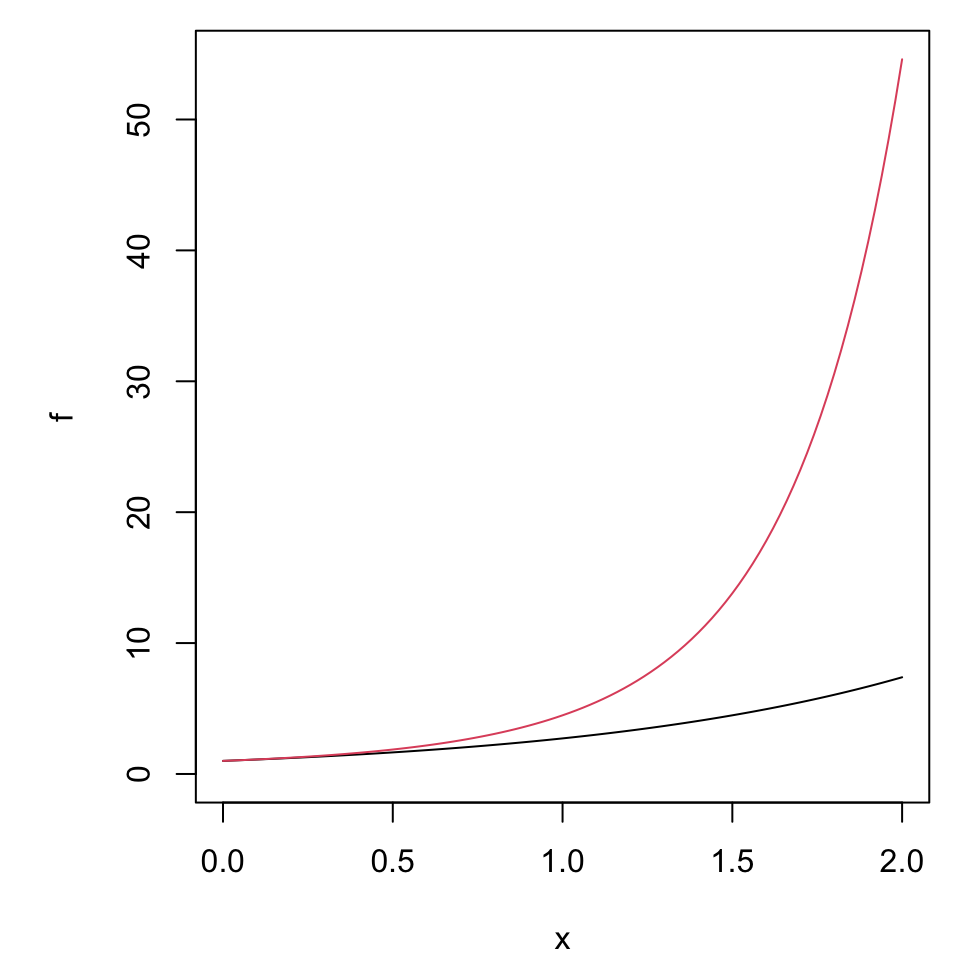
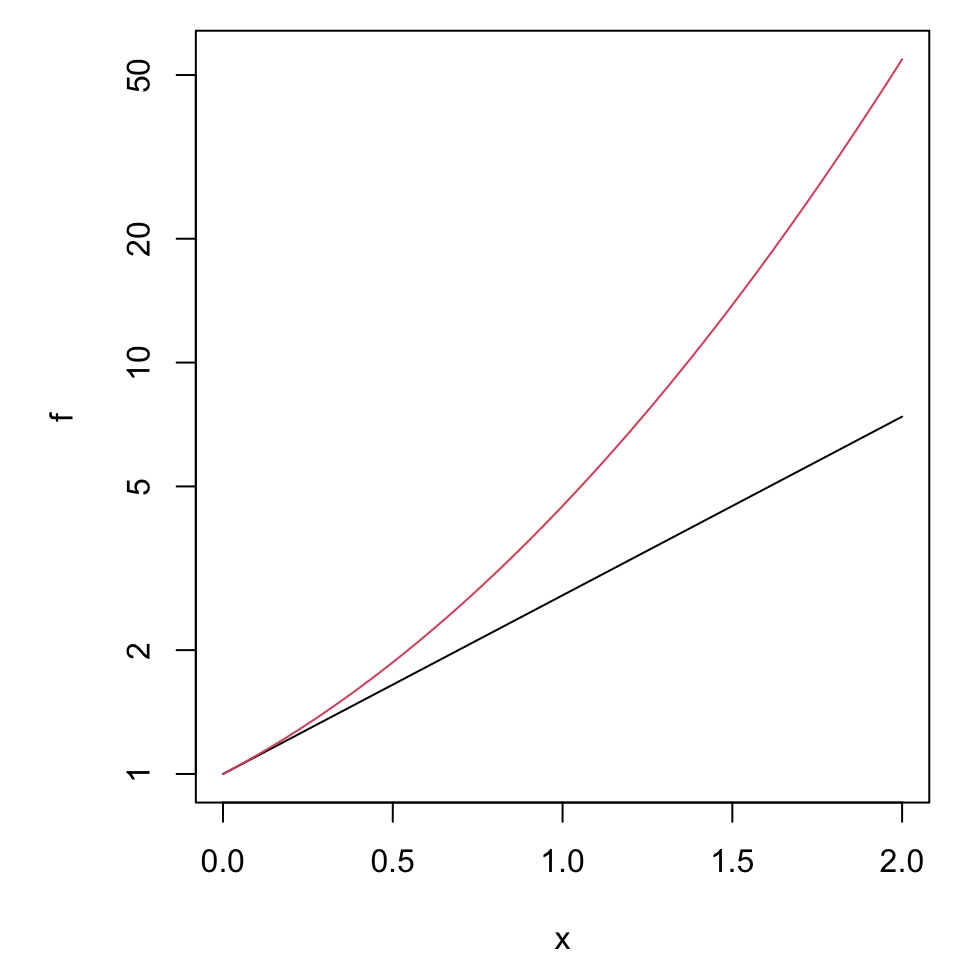
Properties of growth

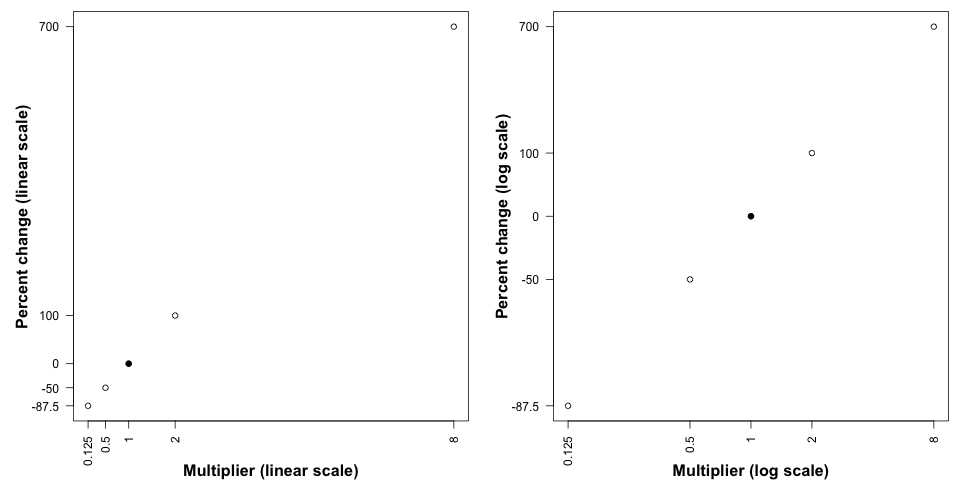
Suppose we are interested in “percent change” as a metric.

Percent change	Multiplier
700%	8
100%	2
0%	1
-50%	\(\frac{1}{2}\)
-87.5%	\(\frac{1}{8}\)

Which is “more important” doubling or halving?
How should each change be represented in a graph?

Spacing

Re-analysis Goals

Graph all three columns of the data in exponential.csv, first on linear scale and next on a log scale.

Observe how the use of vertical space draws attention to the “action” in the data. In other words, “what do you notice?”

Dealing with ugly

The default R axes are not necessarily pleasing.

par(mar = c(4.1, 5.1, 0.8, 0.8))
x <- 0:20
plot(x, 2^(x), ylab = "Doubling of values", xlab = "Number")

As it is, few things will change that.

Changing the scale

The default R axes are not necessarily pleasing.

par(mar = c(4.1, 5.1, 0.8, 0.8))
x <- 0:20
plot(x, 2^(x), ylab = "Doubling of values", xlab = "Number", log = 'y')

New questions

What to plot, what to label?

Do we plot the logarithm and have a “nicer” axis?
Do we plot the raw data and have more complex axis?

Regardless of choice, how do we make it user-friendly and “nice” aesthetically?

Improving aesthetics

Suppress axes with axes = F, but invite them back with the axis() command.

You’ll have to ask and answer

“where are the ticks?”,
“what are their labels?”, and
“what is the vertical axis label?”.

Fortunately we do not have to worry about the horizontal axis (here representing “time”) because that pretty much only makes sense on a linear scale.

par(mar = c(4.1, 5.1, 0.8, 0.8))
x <- 0:20
plot(x, 2^(x), log = 'y')

Options for formatting (base R)

Suppose we wanted to show tick mark labels as powers of ten.

After setting axes = F, we could try a variety of things using axis(). We could

list at locations
list at locations and labels
list at locations and labels (one at a time)

Or we could (and will) use more advanced tools or specialized packages.

A good rule of thumb

To illustrate value use a linear scale, to inspect rate of change use a log scale.

Consider the log-transformation of \(y = ae^{bt}\) which becomes \(\ln(y) = \ln(a) + bt\). (Verify this.)

For convenience we use the natural logarithm, but the rules work the same for any other choice of base.

This means the underlying exponential parameter \(b\) is emphasized as the slope when graphed on the log scale.

Comparing values or growth rates

f <- function(x)exp(x)
g <- function(x)exp((1 + 0.5*x)*x)
par(mar = c(4.1, 5.1, 0.8, 0.8))
plot(f, xlim = c(0, 2), ylim = c(0, g(2)))
plot(g, xlim = c(0, 2), col = 2, add = T)

f <- function(x)exp(x)
g <- function(x)exp((1 + 0.5*x)*x)
par(mar = c(4.1, 5.1, 0.8, 0.8))
plot(f, xlim = c(0, 2), ylim = c(1, g(2)), log = 'y')
plot(g, xlim = c(0, 2), col = 2, add = T, log = 'y')

Other summaries

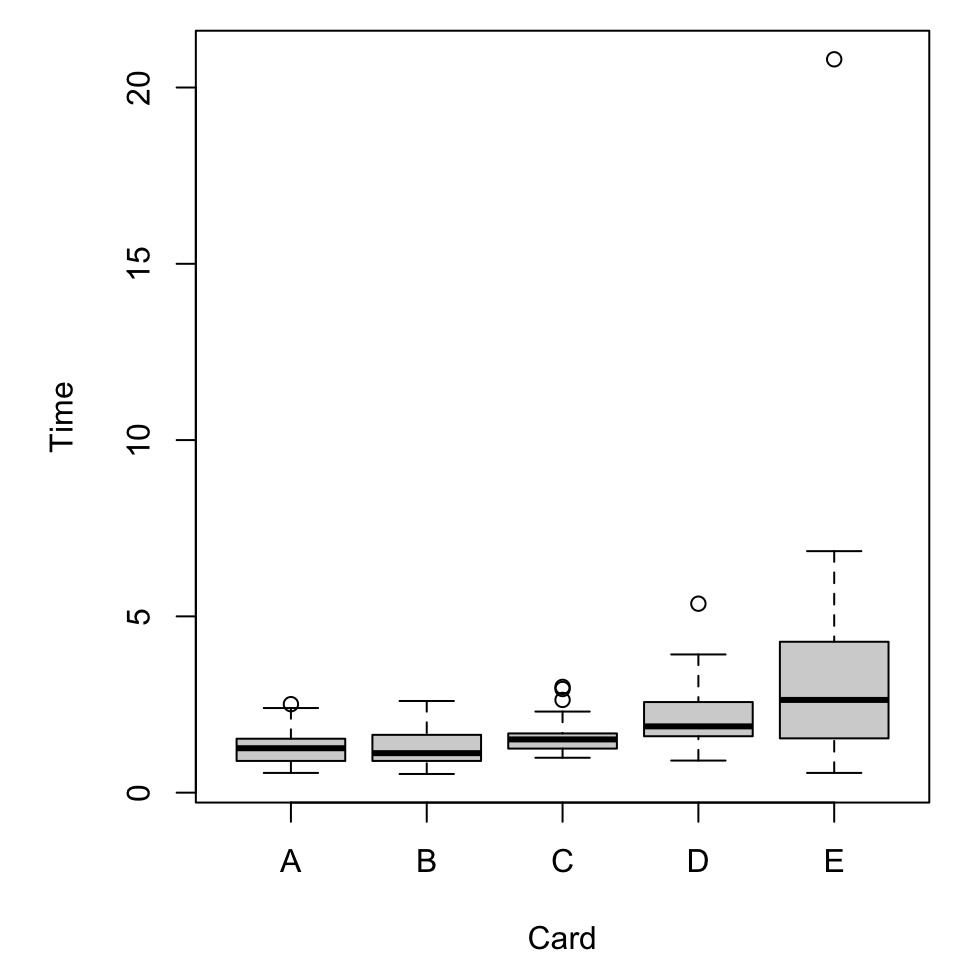
Recall the “preattentive pop-out” data stored in cards.csv.

dat <- read.delim("./data/cards.csv", header = TRUE, sep=',')
dat <- na.omit(dat)
head(dat)
#>   User Card Time
#> 1 hs12    A 1.28
#> 2 hs12    B 1.57
#> 3 hs12    C 1.51
#> 4 hs12    D 1.65
#> 5 hs12    E 6.65
#> 6 br13    A 0.66

What vizualizations are relevant?

Boxplots

A basic boxplot, as we’ve seen, comes pretty quickly.

par(mar = c(4.1, 5.1, 0.8, 0.8))
boxplot(Time ~ Card, dat)

Figure 7: A boxplot of measured reaction times.

What does it mean?

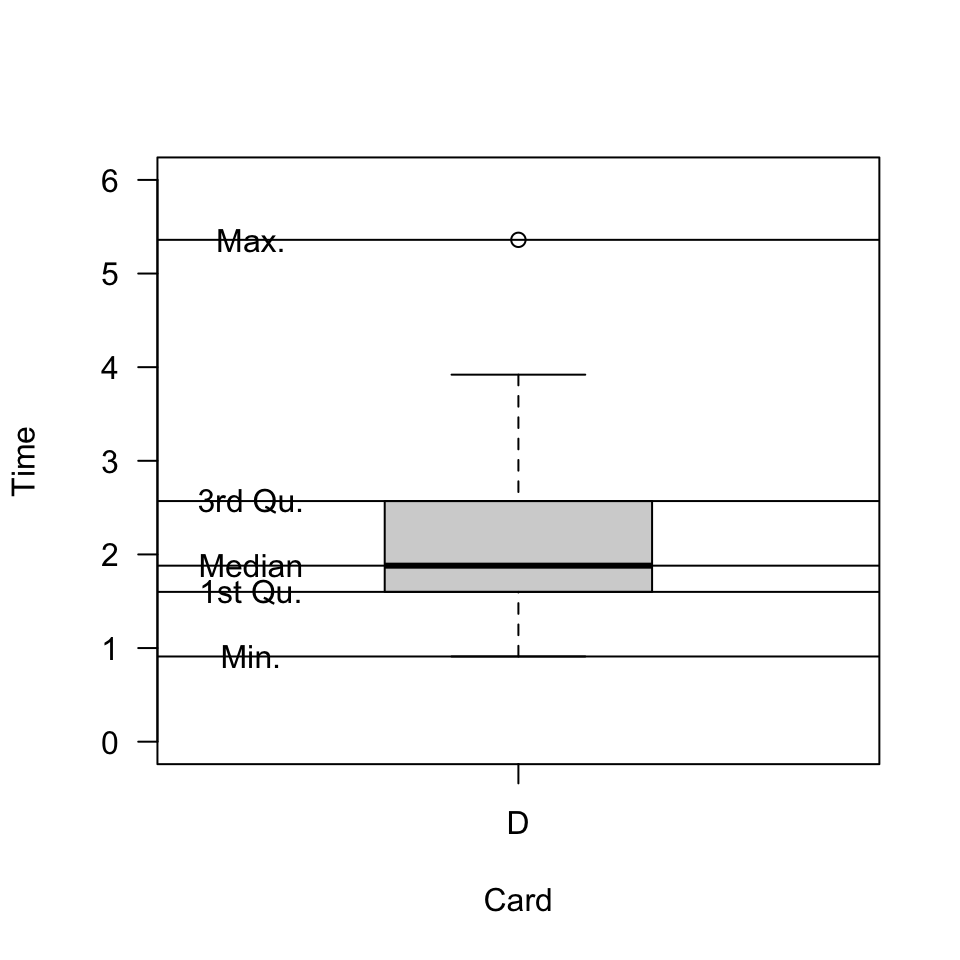
Properties of a boxplot

It might help to know what in our data is reflected in the plot.

summary(dat[dat$Card== "D", "Time"])
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   0.910   1.600   1.880   2.109   2.570   5.360

More categorical variables

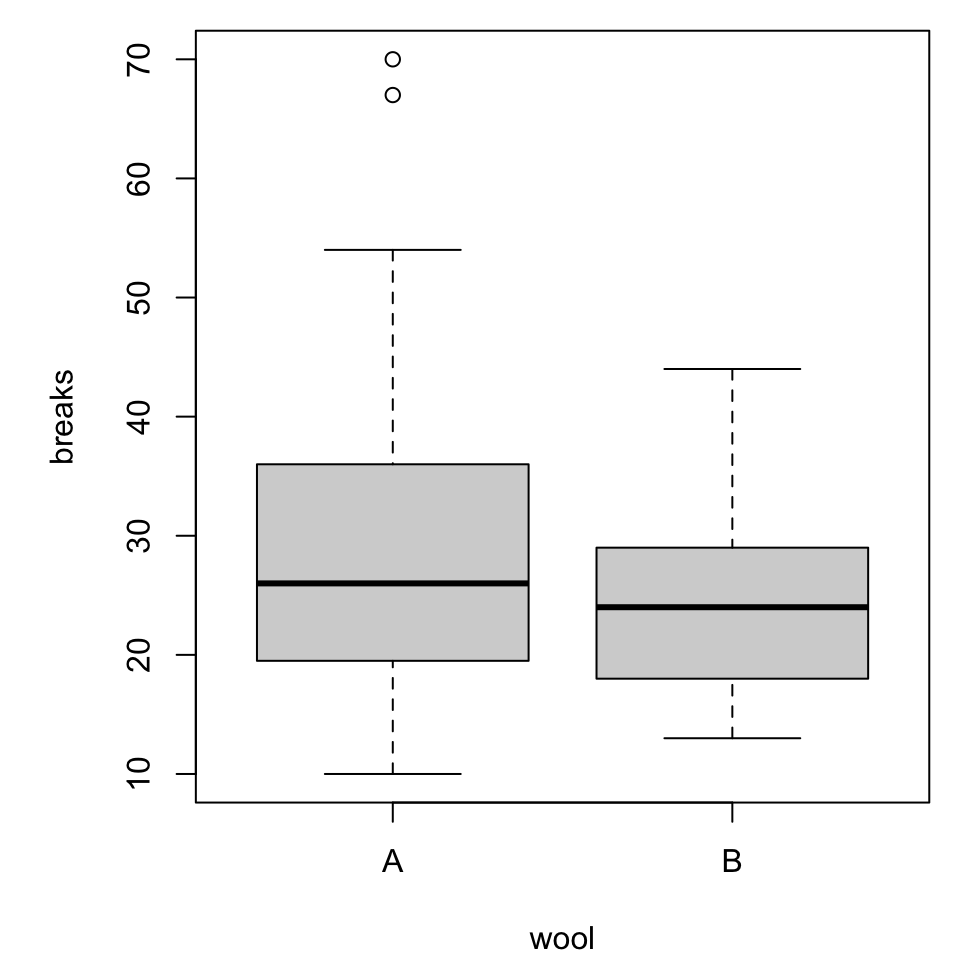
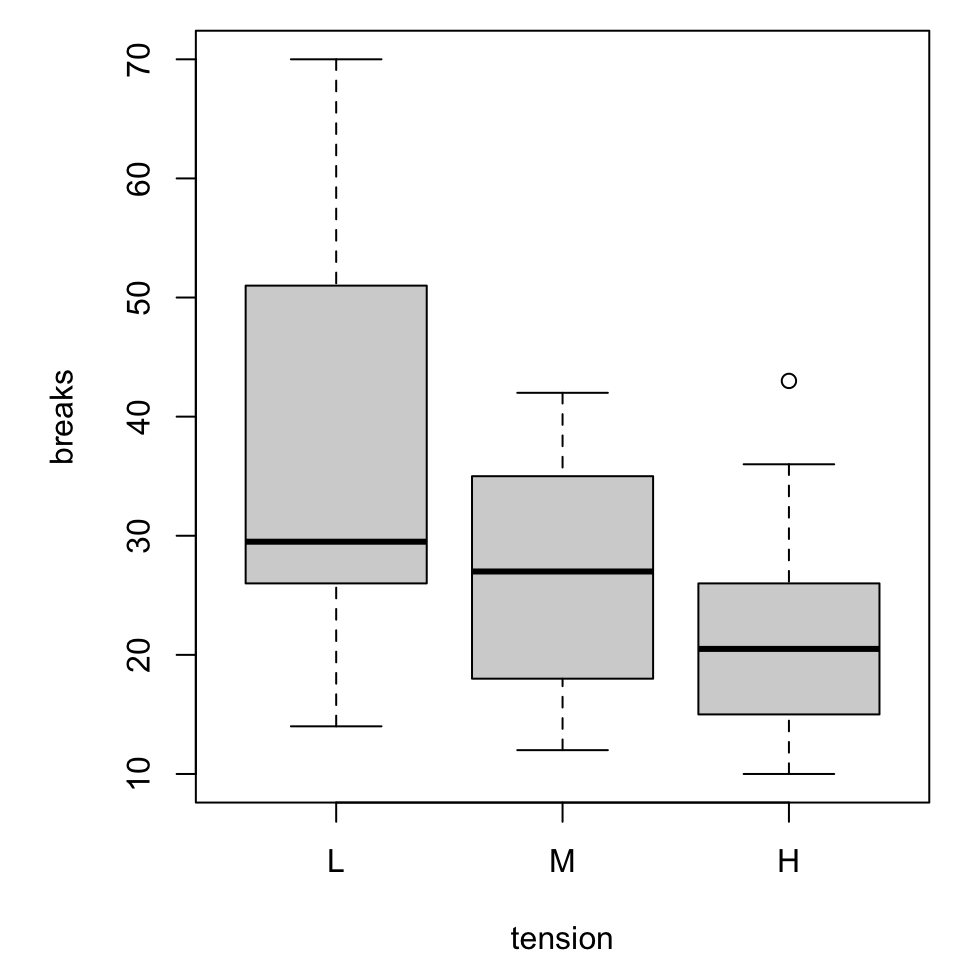
For simplicity we will switch to a built-in dataset, warpbreaks. Use ?warpbreaks to view its description and citation.

Roughly, it contains columns

breaks the number of breaks per length of yarn
wool the type of wool (A or B)
tension the weaving tension (L, M, H)

summary(warpbreaks)
#>      breaks      wool   tension
#>  Min.   :10.00   A:27   L:18   
#>  1st Qu.:18.25   B:27   M:18   
#>  Median :26.00          H:18   
#>  Mean   :28.15                 
#>  3rd Qu.:34.00                 
#>  Max.   :70.00

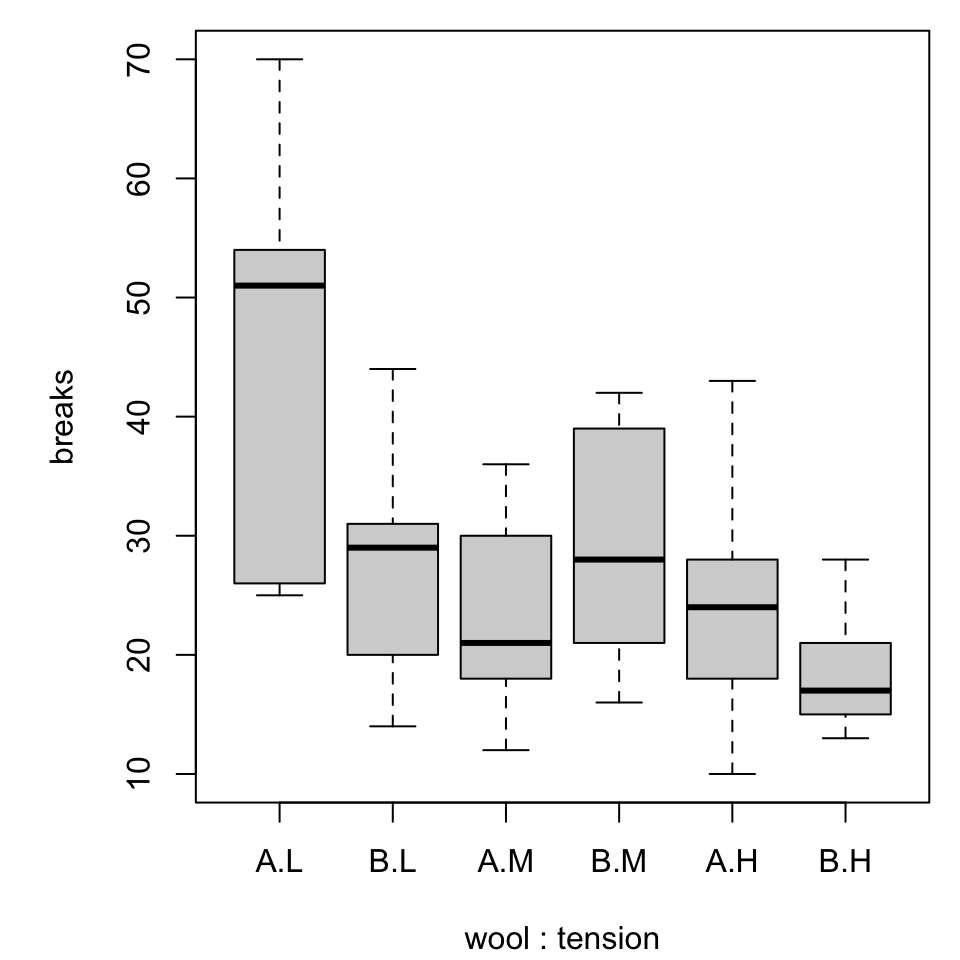
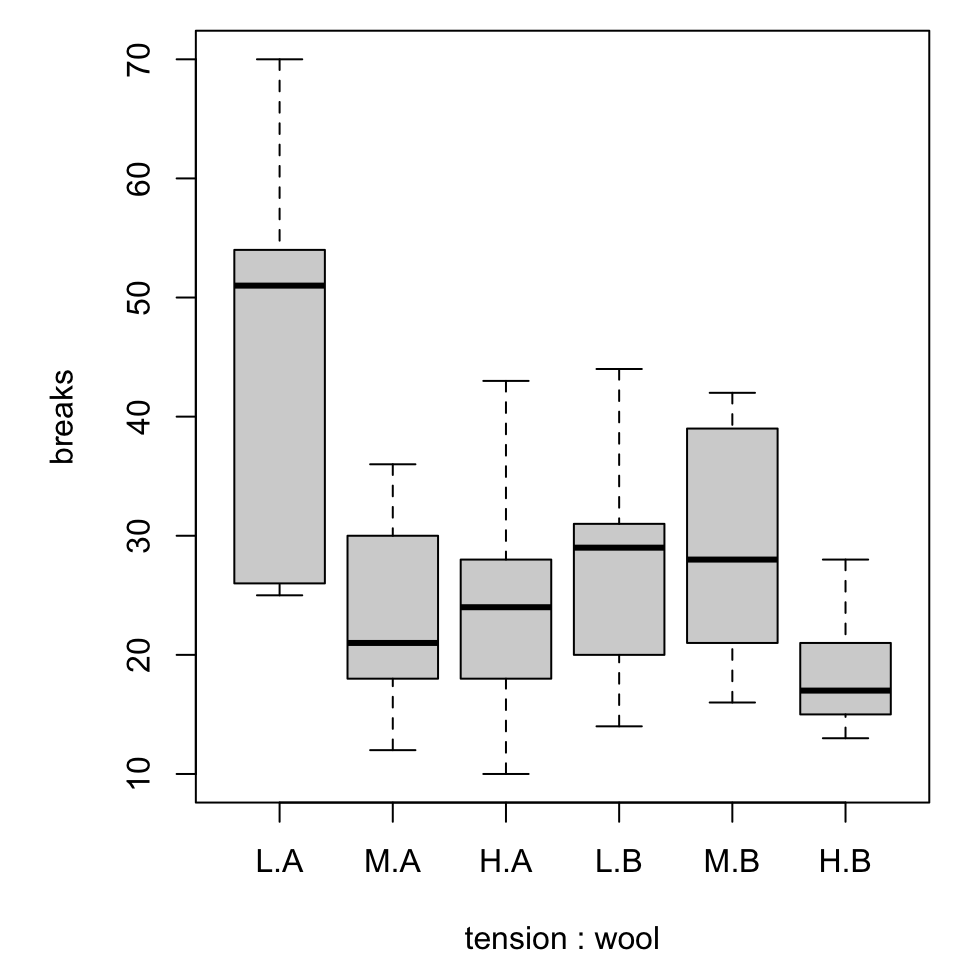
Multiple boxplots

par(mar = c(4.1, 5.1, 0.8, 0.8))
boxplot(breaks ~ wool, warpbreaks)

Figure 8: Number of breaks by wool type.

par(mar = c(4.1, 5.1, 0.8, 0.8))
boxplot(breaks ~ tension, warpbreaks)

Figure 9: Number of breaks by tension setting.

Combined boxplot

Notice that the order of specifying the variables matters!

par(mar = c(4.1, 5.1, 0.8, 0.8))
boxplot(breaks ~ wool*tension, warpbreaks)

Figure 10: Number of breaks by wool type within tension setting.

par(mar = c(4.1, 5.1, 0.8, 0.8))
boxplot(breaks ~ tension*wool, warpbreaks)

Figure 11: Number of breaks by tension setting within wool type.

Annotating boxplots

We could experiment with

replacing the variable codes with meaningful labels
coloring or shading the boxes in helpful ways

There are some interesting features that emerge.

Try specifying two or three colors for the second set of boxplots.
Do the colors appear in a helpful manner?

Extending boxplots

“Recently” boxplots (circa 1977) have evolved into violin plots (circa 1997).

Violin plots show the “shape” of the data.
We will revisit the idea with ggplot.

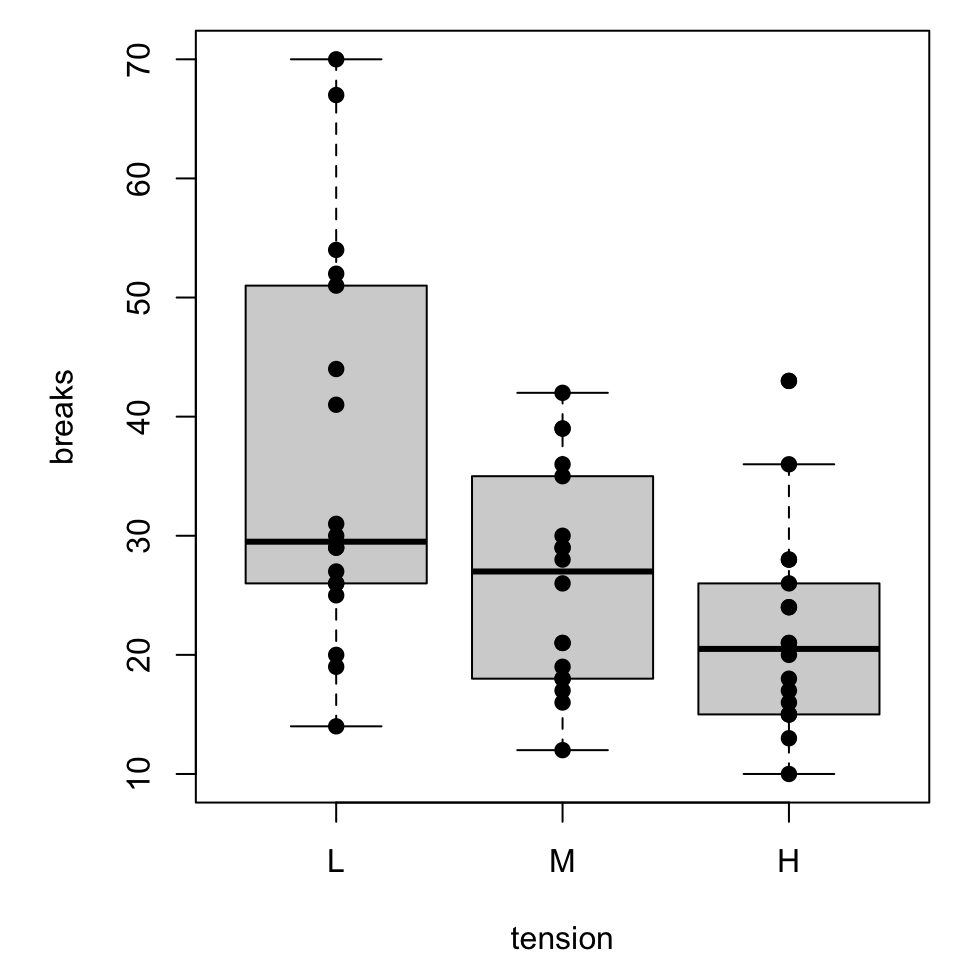
More simply, boxplots can be overplotted with dots.

Boxplot with dots

par(mar = c(4.1, 5.1, 0.8, 0.8))
bxp <- boxplot(breaks ~ tension, warpbreaks)
points(breaks ~ tension, warpbreaks, pch = 19)

Figure 12: Number of breaks by tension setting within wool type. Raw data added.

Since many of the dots might overlap, we might be interested in incorporating horizontal jitter to alter the readability

Things get a little slippery here.

tension and wool are categorical, so it might take a bit of scratchwork to determine sensible, numerical input values.
It would be reasonable to create auxilliary variables that are numerical analogs (i.e., L “=” 1, M “=” 2, …).

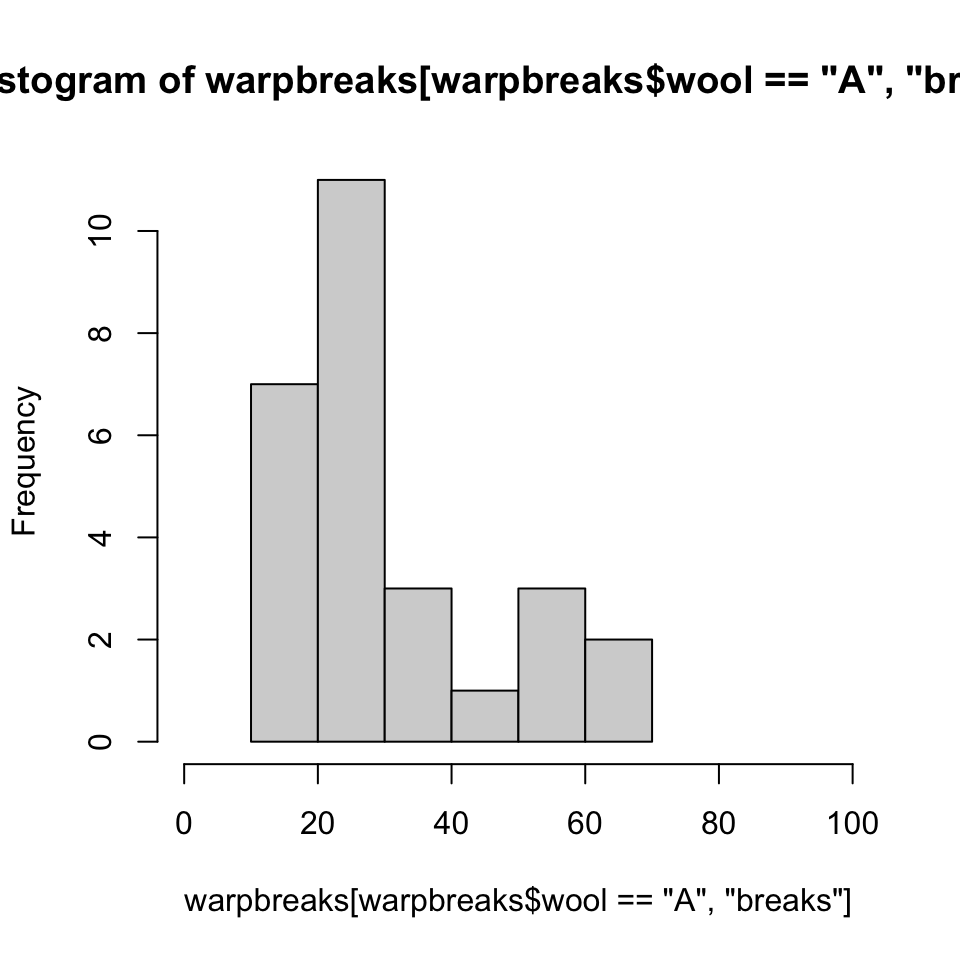
Histograms

The boxplot easily shows some major summary statistics. Sometimes we want more resolution.

hst <- hist(warpbreaks[warpbreaks$wool == "A", "breaks"], xlim = c(0, 100))

Figure 13: Number of breaks by tension setting within wool type. Raw data added.

A few comments:

The main title, provided for free based on arguments provided, is ugly.
“Frequency” on the vertical axis means “count”, we get that by specifying freq = TRUE (or nothing).
For a probability “Density” we set freq = FALSE. This scales the graph to an AUC of one.
Saving the result to hst (NOT “hist”) allows us to peek at the numerical properties.

Why an AUC of one?

It is possible to “smooth” a histogram by computing a “kernel density estimate”, analogous to an empirically-generated “probablity density function”.

The density() command is worth some independent investigations if it it interests you.

density(warpbreaks[warpbreaks$wool == "A", "breaks"], from = 0, to = 100)
#> 
#> Call:
#>  density.default(x = warpbreaks[warpbreaks$wool == "A", "breaks"],     from = 0, to = 100)
#> 
#> Data: warpbreaks[warpbreaks$wool == "A", "breaks"] (27 obs.);    Bandwidth 'bw' = 5.733
#> 
#>        x             y            
#>  Min.   :  0   Min.   :3.000e-09  
#>  1st Qu.: 25   1st Qu.:1.851e-03  
#>  Median : 50   Median :6.585e-03  
#>  Mean   : 50   Mean   :9.956e-03  
#>  3rd Qu.: 75   3rd Qu.:1.551e-02  
#>  Max.   :100   Max.   :3.152e-02

That could be

inspected as is,
plotted with plot(), or
superimposed on an earlier histogram by using plot(..., add = T).