Class 9 notes

Author

Sean Laverty

Published

April 30, 2025

Warning

Before you run this, be sure you have a directory called “csvs/” in this folder. If you using this downloaded copy, you will. But, in future tasks to repeat the final step you would need to ensure that the folder exists. This is used to create the filenames (and paths) for the output .csv files.

Layout

Using the layout() command, we can create nice layouts. With ggplot2 you can use the package gridExtra for comparable options.

layout(matrix(c(1, 1, 2, 1, 1, 2, 3, 3, 4), nrow = 3, ncol = 3, byrow = TRUE))
par(mar = c(4.1, 5.1, 0.8, 0.8))
plot(1:25, pch = 1:25, col = hcl.colors(25))
plot(runif(100, 0, 1))
plot(sin, xlim = c(0, 2*pi))
plot(cos, xlim = c(0, 2*pi))

Figure 1: Random content in a nice plot layout.

2016 Rio Olympics data

Now we will read in the Olympics data.

dat <- read.csv("./data/athletes.csv")
head(dat)

         id           name nationality    sex date_of_birth height weight
1 736041664 A Jesus Garcia         ESP   male    1969-10-17   1.72     64
2 532037425     A Lam Shin         KOR female    1986-09-23   1.68     56
3 435962603    Aaron Brown         CAN   male    1992-05-27   1.98     79
4 521041435     Aaron Cook         MDA   male    1991-01-02   1.83     80
5  33922579     Aaron Gate         NZL   male    1990-11-26   1.81     71
6 173071782    Aaron Royle         AUS   male    1990-01-26   1.80     67
      sport gold silver bronze info
1 athletics    0      0      0     
2   fencing    0      0      0     
3 athletics    0      0      1     
4 taekwondo    0      0      0     
5   cycling    0      0      0     
6 triathlon    0      0      0

To calculate ages, we can append columns of the start date of the 2016 Rio Olympics and the participant’s julian birthday. From those we can calculate the age in days as their difference. Dividing that by 365¹, we can approximate each participant’s age in years. You can probably do this a little more carefully with the lubridate package, since our current approach overlooks the existence of leap years.

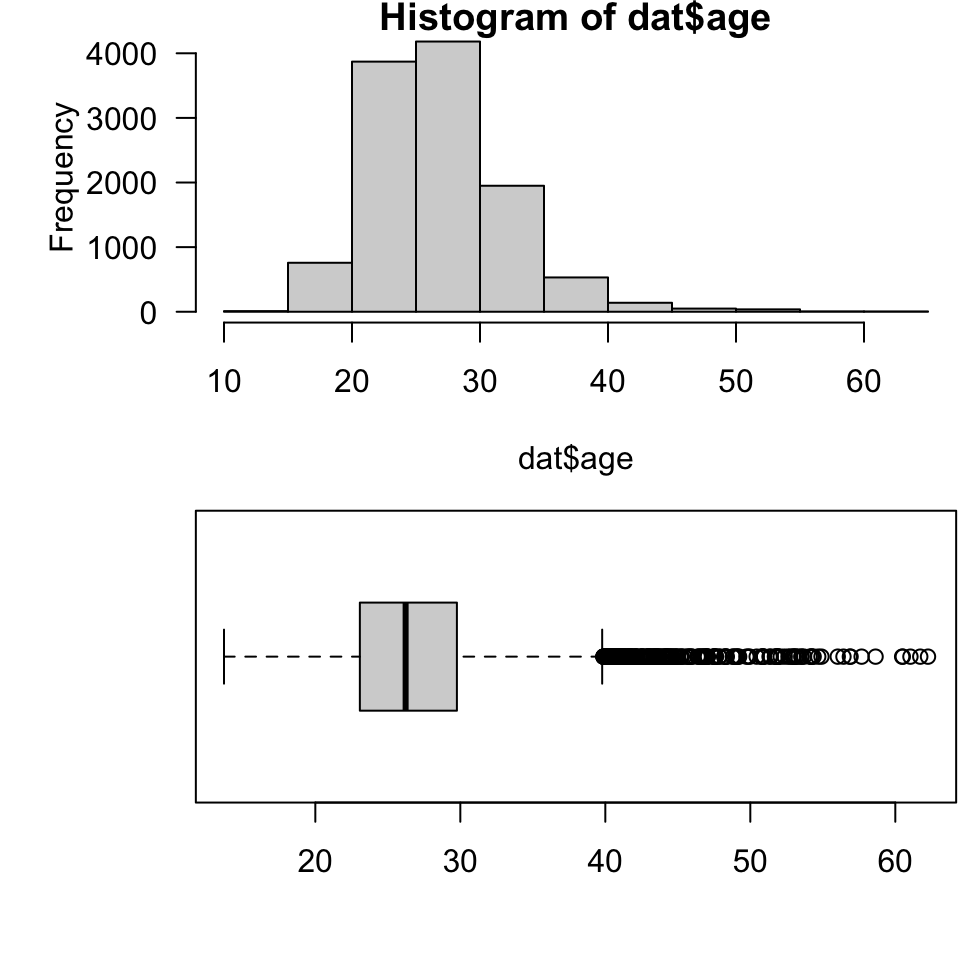
dat$start <- julian(as.Date("2016-08-05", "%Y-%m-%d"))
head(dat$start)

[1] 17018 17018 17018 17018 17018 17018

dat$bday <- julian(as.Date(dat$date_of_birth, "%Y-%m-%d"))
head(dat$bday)

[1]  -76 6109 8182 7671 7634 7330

dat$age <- dat$start - dat$bday
dat$age <- dat$age/365
head(dat$age)

[1] 46.83288 29.88767 24.20822 25.60822 25.70959 26.54247

Just to check, it is nice to explore visualizations of the distribution of calculated ages. If nothing else this gives us to chance to rule out unreasonable values. For example, say we wrote but didn’t execute the line above dividing the age in days by 365.

par(mfrow = c(2, 1), mar = c(4.1, 5.1, 0.8, 0.1))
hist(dat$age, las = 1)
boxplot(dat$age, horizontal = T, las = 1)

Figure 2: Random content in a nice plot layout.

Now we can calculate, as an example of a reasonable task, the Olympians over 50 years old at the start of the games. After making that data subset (which could have been done with something like dat2 <- subset(dat, subset = age > 50)). After that we expore the corresponding nationalities and sports to make a table of their frequencies of co-occurring.

dat2 <- dat[dat$age > 50, ]
dim(dat2)

[1] 48 15

head(dat2[ , c("nationality", "sport")])

     nationality      sport
33           MAR equestrian
56           IOA   shooting
1377         ESP equestrian
2056         PLE equestrian
2232         CAN   shooting
2381         COL   shooting

dat3 <- as.data.frame(table(dat2[ , c("nationality", "sport")]))
head(dat3)

  nationality      sport Freq
1         ANG equestrian    0
2         ARG equestrian    0
3         AUS equestrian    4
4         BEL equestrian    1
5         BRA equestrian    0
6         CAN equestrian    0

dat3 <- dat3[dat3$Freq > 0, ]

After keeping only the combinations of sports and nationalities that occur, we quickly write each to a text file. There are a number of circumstances under which this exact task, or something quite structurally-similar, would be useful. These particular output files are not very interesting, but this serves still as a good example of “dynamic filenames”. You could use the same “paste a variable value” technique for labeling graphs.

dat3 <- dat3[order(dat3$Freq, decreasing = TRUE), ]
nms <- levels(dat3$nationality)
nms

 [1] "ANG" "ARG" "AUS" "BEL" "BRA" "CAN" "COL" "ESP" "FIJ" "FRA" "GBR" "GER"
[13] "IOA" "LUX" "MAR" "NZL" "PAN" "PAR" "PER" "PLE" "POR" "RUS" "SUI" "SWE"
[25] "USA" "VEN"

for(n in nms) write.csv(dat3[dat3$nationality == n, ], paste("./csvs/", n, ".csv", sep = ""), row.names = FALSE)

Footnotes

overlooking leap years↩︎